Групповая оценка объектов
Следует заметить, что практическое вычисление векторов групповой оценки объектов и коэффициентов компетентности проще выполнять по рекуррентным формулам (5.4), (5.5), (5.6). Определение предельных значений этих векторов по уравнению (5.13) требует применения вычислительной техники.
Рассмотрим теперь случай, когда эксперты производят оценку множества объектов методом ранжирования так, что величины  есть ранги. Обработка результатов ранжирования заключается в построении обобщенной ранжировки. Для построения такой ранжировки введем конечномерное дискретное пространство ранжировок и метрику в этом пространстве. Каждая ранжировка множества объектов j-м экспертом есть точка
есть ранги. Обработка результатов ранжирования заключается в построении обобщенной ранжировки. Для построения такой ранжировки введем конечномерное дискретное пространство ранжировок и метрику в этом пространстве. Каждая ранжировка множества объектов j-м экспертом есть точка 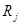 в пространстве ранжировок.
в пространстве ранжировок.
Ранжировку 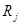 можно представить в виде матрицы парных сравнений, элементы которой определим следующим образом [12]:
можно представить в виде матрицы парных сравнений, элементы которой определим следующим образом [12]:

Очевидно, что  , поскольку каждый объект эквивалентен самому себе. Элементы матрицы
, поскольку каждый объект эквивалентен самому себе. Элементы матрицы  антисимметричны
антисимметричны  .
.
Если все ранжируемые объекты эквивалентны, то все элементы матрицы парных сравнений равны нулю. Такую матрицу будем обозначать  и считать, что точка в пространстве ранжировок, соответствующая матрице
и считать, что точка в пространстве ранжировок, соответствующая матрице  , является началом отсчета.
, является началом отсчета.
Обращение порядка ранжируемых объектов приводит к транспонированию матрицы парных сравнений.
Метрика 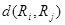 как расстояние между i-й и j-й ранжировками определяется единственным образом формулой [12]
как расстояние между i-й и j-й ранжировками определяется единственным образом формулой [12]

если выполнены следующие 6 аксиом [12]:
1.  причем равенство достигается, если ранжировки
причем равенство достигается, если ранжировки 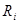 и
и 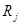 тождественны;
тождественны;
2. 
3. 
причем равенство достигается, если ранжировка «лежит между» ранжировками 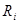 и
и 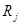 . Понятие «лежит между» означает, что суждение о некоторой паре
. Понятие «лежит между» означает, что суждение о некоторой паре  объектов в ранжировке совпадает с суждением об этой паре либо в
объектов в ранжировке совпадает с суждением об этой паре либо в 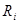 , либо в
, либо в 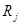 или же в
или же в 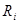
 в
в 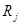
 а в
а в 

Перейти на страницу:
1 2 3 4 5 6